MÖBIUSOV ŠAH

O geometriji, topologiji i šahovskoj igri

Premda se geometrijsko stvorenje poznato pod nazivom möbiusova vrpca nekome može činiti kao puka
zanimljivost, neka vrsta kurioziteta među stvorenjima ove vrste, ono u matematici, odnosno geometriji ima
vrlo velik značaj. Taj značaj možemo vidjeti recimo na primjeru teorema o topološkoj klasifikaciji zatvorenih
dvodimenzionalnih ploha u kojemu se zajedno sa sfernom i toroidalnom površinom površinama
kugle odnosno torusa möbiusova vrpca koristi pri opisu svih mogućih takvih ploha (ograničenih dvodimenzionalnih "površina") koje postoje odnosno mogu postojati na svijetu. Također, to je jedan od primjera plohe koja se "neprekidnim deformacijama" ne može "smjestiti" u ravninu, a iz dvije möbiusove vrpce može se kreirati, ili bi možda bolje bilo reći zamisliti, jedno još čudnije stvorenje, koje zovu kleinova boca, ploha koja se ne može "smjestiti" u ovaj naš trodimenzionalni prostor, već joj za "normalan život" treba jedna dimenzija više.
Ako niste shvatili ništa od ovoga što je dosada rečeno nema veze. Krenut ćemo ispočetka i najprije, za one
koji ne znaju, reći što je to uopće möbiusova vrpca. Dakle, möbiusova vrpca je ploha koja nastaje lijepljenjem dviju nasuprotnih stranica pravokutnika jedne uz drugu i to tako da ako vrhove pravokutnika označimo redom (recimo smjerom suprotnim od smjera kretanja kazaljki na satu) sa A, B, C, D, onda točku A lijepimo uz C i B uz D (primjetimo da lijepljenjem A uz B i C uz D dobivamo cilindar), što znači da jednu stranicu pravokutnika
najprije treba "preokrenuti" odnosno "izvinuti", pa tek onda slijepiti uz drugu stranicu. Ova "ploha" za razliku
od cilindra ima samo jedan rub i jednu "stranu"1. Zgodno je da čitatelj od papira napravi jednu möbiusovu
vrpcu i sam se uvjeri da je ovo što je o njoj rečeno istina. Kome je to lijeno, neka nešto pokuša dokučiti iz
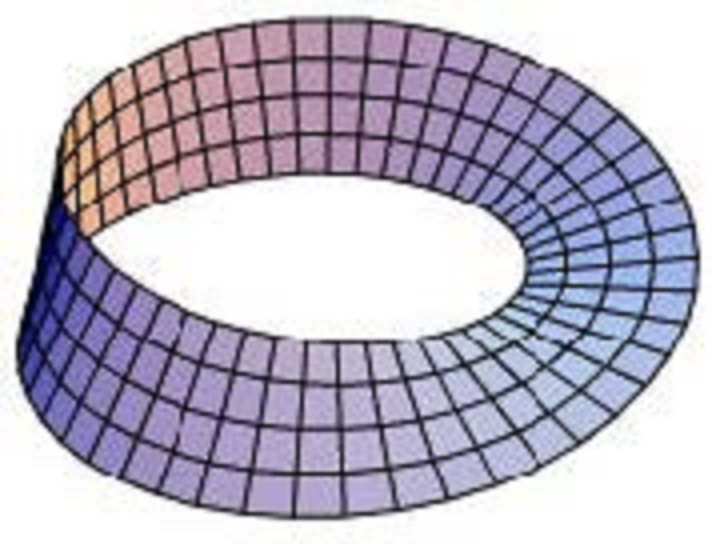
slijedeće slike:

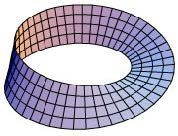
Sl.1 Möbiusova
vrpca
(preuzeto iz Wikipedije)

Kakve sad ovo, gore rečeno, ima veze sa šahovskom igrom i što uopće znači formulacija "möbiusov šah" iz
naslova ove priče? Ima veze zbog toga što se šah može igrati i na möbiusovoj vrpci. Zašto bismo uostalom šah
igrali samo na komadu euklidske ravnine kvadratnog oblika koji je "pravilno" podijeljen na 8x8 polja?
Možemo ga igrati i na cilindru, i na kugli i na möbiusovoj vrpci, a na koncu i na gore spomenutoj klajnovoj boci, samo što mi se ovo zadnje čini prekompliciranim, pa se time, barem zasad, ne mislim baviti. Vjerojatno su ljudi na ovakve ideje došli već odavno. Za sebe samog mogu reći kako sam prvo smislio nešto što se zove "okrugli šah", a to je zapravo šah na cilindru, pa onda nije trebalo puno da mi padne na pamet i ideja za šah na möbiusovoj vrpci, odnosno na drugim dvodimenzionalnim plohama koje se međusobno razlikuju po svojoj topologiji2.
Možda će sada neki okorjeli šahist prigovoriti da je sve to sigurno bez veze, jer već i sama činjenica da se o
takvim stvarima uopće ne priča, navodi na zaključak da to mora biti nešto bez veze. Da li je ili nije, ne znam,
mogu reći da sam odigrao dosta partija "okruglog šaha" i da je dojam koji je na mene ova igra ostavila prilično

1 Möbiusova vrpca k tomu nije nije orijentabilna, što znači da na takvoj plohi nije moguće definirati smjer
vrtnje kao globalan pojam (dokaz ove tvrdnje prepuštamo ambicioznijim čitateljima).

2 U vezi pitanja Što je topologija? zainteresirani
čitatelj može konzultirati odgovarajuću literaturu. Mi
možemo navesti njenu definiciju koju je dao jedan od njezinih utemeljitelja, francuski matematičar Henri
Poincare (18541912)
"
Topologija je znanost koja se bavi kvalitativnim svojstvima geometrijskih objekata, ne samo onih u "običnom" prostoru, već i onih u prostoru sa više od tri dimenzije".
1
blijed3. Njezin je problem, naime, višestruko povećana moć teških figura koje mogu istovremeno napasti s
dvije strane, zbog čega igra obično gubi na dinamici, a mogućnosti za efektne i iznenađujuće akcije znatno su
sužene. Što se tiče möbiusovog šaha, moram priznati da tu nemam nekog iskustva, za takvo što ne uspijevam
pronaći niti suparnika, niti vlastito vrijeme.
No, poanta ove priče nije u šahu, nego u matematici. Ona leži u jednoj matematičkoj odnosno geometrijskoj
začkoljici na koju sam slučajno naletio u vrijeme dok sam se zabavljao razmatranjem ove varijante šahovske
igre, i uvjeren sam da će taj problem zainteresirati sve one koji uživaju u rješavanju matematičkih zadataka.
Da bismo došli do toga problema, najprije je potrebno potruditi se oko definiranja igre koja će se zvati
"möbiusov šahom", odnosno postuliranja njezinih pravila. Za ovaj posao poslužit ćemo se, dakako, definicijom i pravilima "normalnog šaha". Evo jedne moguće definicije koja mi je prvotno pala na pamet:
"Uzmimo običnu šahovsku ploču na koju su figure poslagane normalno i od nje kreirajmo möbiusovu vrpcu preokrenimo recimo crnu stranu i slijepimo linije 1 i 8 a1 se lijepi uz h8, b1 uz g8, ... , h1 uz a8. Pošto se
crno polje a1 lijepi iz crno polje h8, nameće se ideja da stavimo još jedan redak (9) da bismo osigurali
pravilan slijed crnobijelih polja (inače kretanje lovaca ne bi bili ograničeno samo na crna odnosno samo
na bijela polja) Sada se figure "fizički" nalaze na različitim "stranama" ploče ako kažemo da bijele figure
stoje normalno (uspravno), onda crne stoje "naglavačke". Lako se vidi da se topovi napadaju međusobno, a da svaka kraljica napada suprotnog kralja, pa je zgodno dodati još po jedan red bijelih i crnih pješaka s druge strane figura koji sprečavaju ove napade. No, udaljenost redaka sa figurama u ovom slučaju iznosi s jedne strane 4 polja a s druge 8, pa ćemo crnu vojsku pomaknuti za dva polja "unazad" tako da udaljenosti među figurama budu iste (6 polja). Ako sada još kažemo da se figure kreću na isti način kao u normalnom šahu potpuno smo definirali igru koju možemo nazvati "šahom na möbiusovoj vrpci" ili " möbiusovim šahom", pri čemu ostaje još možda jedino pitanje unaprijeđenja pješaka koji nikada ne može stići do ruba ploče."
Međutim, kad sam malo detaljnije proučio ovu definiciju, uočio sam jednu njezinu fatalnu grešku zbog koje se tako definirana igra nikako ne bi smjela zvati "möbiusovim šahom" već nekako drugačije. Čitalac za zadaću treba pronaći u čemu je ta greška, tj. treba dokazati da prostor na kojemu se odvija opisana igra uopće nije möbiusova vrpca, identificirati taj prostor, skicirati šahovsku ploču sa početnim položajem figura u ovoj "krivo definiranoj" odnosno nazvanoj igri (koja se opet može smatrati jednom novom varijantom šahovske igre), te dati nov, ispravan opis "šaha na möbiusovoj vrpci". Pritom ponovno sugeriramo čitateljima da od papira naprave model möbiusove vrpce, a prije "lijepljenja" na tome modelu, odnosno papirnoj traci skiciraju šahovska polja. Oni kojima je to lijeno, neka se ponovno pokušaju poslužiti slikom 1, na kojoj se nacrtane kockice mogu prispodobiti šahovskim poljima.

3 Okrugli šah nastaje tako da normalnu šahovsku ploču sa normalnim početnim rasporedom figura "slijepimo" po linijama a i h dakle polje a1 "lijepimo" uz polje h1, polje a2 uz polje h2, ... , polje a8 uz
polje h8. Jasno je da na taj način dobivamo cilindričnu ploču kod koje su figure poslagane po rubovima.
Taj cilindar možemo "projicirati" na ravninu (cilindar se za razliku od möbiusove vrpce može neprekidnim defirmacijema "smjestiti" u ravninu, pa ploču za ovu igru možemo predstaviti krugom bez središnje točke (radi se zapravo o kružnom vijencu), pri čemu šahovska polja omeđuje niz od 8 koncentričnih kružnica i pramen od 4 simetrično postavljena pravca koji se sijeku u središtu kruga dijeleći ga "na kriške" (njih 8). Figure su ovdje smještene uz rub i oko središta kruga (ovo bi trebalo nacrtati).

2
Rješenje problema (okrenuti naopako)

Stvar je u tome što smo drugu (donju) stranu ploče uzeli kao dodatni dio ploče, i tako dvije "strane" möbiusove
vrpce proglasili zasebnim "područjima" koja lokalno nisu povezana ("antipodne" točke povezane su tek
linijama čija je minimalna duljina jednaka polovici duljine jedinstvenog ruba vrpce). A ako möbiusovu vrpcu na taj način "dupliramo", ono što ćemo dobiti više neće biti möbiusova vrpca.
Zaista, prema opisanoj konstrukciji ploče, slijedi da se a linija ploče nastavlja na h liniju (h linija sa suprotne
strane ploče) iza a9 slijedi h1, pa onda idu h polja do h9
iza kojega slijedi a1! Analogno duž drugog ruba
imamo slijed h1, ..., h9, a1, ..., a9, pa onda opet h1. Dakle ovdje imamo dva (nepovezana) ruba koji predstavljaju rubove "cilindra" koji nastaje tako da jedan od "kraćih" rubova pravokutnika dimenzije 8x18 polja četiri puta "preokrenemo" i onda slijepimo sa drugim "kraćim" rubom (a1 zalijepimo uz a18=h9, ... , h1 uz h18=a9).
Ovu tvrdnju možemo provjeriti tako da model möbiusove vrpce napravimo od dvije papirne trake koje se poklapaju preokrenemo jedan njihov rub, zalijepimo ih sa obje strane i onda stvar "raširimo".
"Profil" duplirane möbiusove vrpce prikazan je na slijedećoj slici:

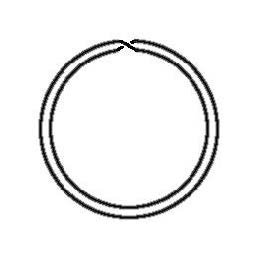
Sl. 2 Duplirana
möbiusova vrpca (gledano "iz profila")

Ovdje se radi o paradoksu je sličnom onome kod kojega se tvrdi da je površina möbiusove vrpce dvostruko
veća od površine pravokutnika od koje je vrpca nastala jer joj je širina jednaka širini pravokutnika, a duljina
jednaka dvostrukoj dužini jer trebamo prevaliti put dvostruko dulji od dužine pravokutnika da bismo se
vratili u istu točku. Štos je, naravno, u tome da smo se već nakon pola puta našli u toj točki, ali sa "suprotne
strane", pa to nismo ni primijetili. Naravoučenije ovog razmatranja je u tome da kad bismo "fizički" htjeli
napraviti möbiusovu šahovsku ploču onu "vjernu" u tri dimenzije, jer se möbiusova vrpca, kako smo već
rekli ne može neprekidnim deformacijama (matematičari bi rekli homeomorfno) "smjestiti" u manje od tri dimenzije trebali bismo koristiti proziran materijal, jer bi se u suprotnom (zbog nepažnje) moglo dogoditi da se na istom polju nađu dvije figure, a mi to ne primjetimo jer je jedna s jedne strane, a druga s druge. Dakako, prozirna ploča davala bi i daleko bolji pregled pozicije nego ona "neprozirna".
Sama ploča može se napraviti tako da uzmemo pravokutnik dimenzija 8*18 polja, jedan njegov kraći rub
"preokrenemo" i onda slijepimo s drugim kraćim rubom dakle polje a1 lijepimo uz h18, ..., h1 uz a18.
Primjetimo da su polja a1 i h18 crna, odnosno da su b1 i g18 bijela, itd. Da bismo osigurali pravilan slijed
crnobijelih polja, ploča, kako smo vidjeli ranije, mora imati neparan broj polja, pa bismo joj morali ili dodati
ili oduzeti jedan redak (kao što smo ranije dodali deveti). No u tom slučaju dolazimo do nesimetrične situacije u kojoj udaljenosti figura s jedne i s druge strane nisu jednake. Tako upadamo u dilemu hoćemo
li imati neparan broj redaka, dakle pravilan slijed crnobijelih polja i "nesimetričnu situaciju" ili ćemo imati paran broj redaka i simetričnu situaciju, ali istovremeno narušen slijed crnobijelih polja, što znači, uz ostalo, da kretanje lovaca više neće biti ograničeno samo na crna, odnosno samo na bijela polja. Pošto broj 144 ima određenu simboličku vrijednost, čini mi se zgodnijim uzeti ploču od 18 redaka, dakle sa simetričnom situacijom, no neka čitatelj odluči sam. Najzgodnije bi zapravo bilo isprobati jedan i drugi slučaj u konkretnoj igri.
3
Dodatno razmatranje

Razmotrimo projekciju möbiusove šahovske ploče u dvije dimenzije. Ploču dimenzija 8x18 možemo "izvinuti"
po duljoj stranici u kružni interval čiji se (kraći) rubovi ne mogu spojiti "regularno", već se taj "spoj" (redaka 1
i 18) u dvije dimenzije može prikazati kao jedna točka u kojoj "vanjska" linija (a) prelazi u "unutrašnju" (h) i
obratno i tako dalje. Točnije, linija a u a18 "nastavlja se" iza te točke na liniju h u h1, linija b u b18 "nastavlja
se" na liniju g u g1, ..., linija h u h18 nastavlja se na liniju a u a1. Dakle, projekcija möbiusove ploče na
ravninu izgleda ovako (na slici je prikazana samo "topologija" ove projekcije, bez crnobijelih
polja):

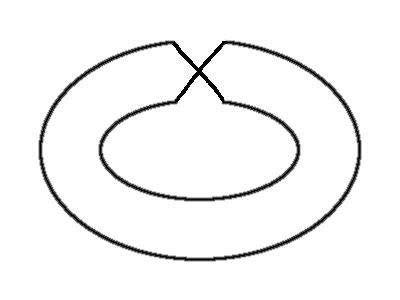
Sl. 3 Projekcija
möbiusove šahovske ploče na ravninu

Točku u kojoj nastaje prijelaz iz jedne linije u drugu možemo nazvati "singularitetom" na ploči. Jasno je da
zbog ove točke pregled situacije na ploči postaje prilično "mutan", no to se u dvije dimenzije ne može izbjeći.
Primijetimo da je singularitet zapravo potrebno staviti na spoj 5. i 6. ili 14. i 15. retka da bismo imali
simetričnu situaciju u slučaju da su figure na ploču složene onako kako je to ranije opisano (u 1. odnosno 10.
redak itd.).
Pitanje koje se nameće samo po sebi je Što se događa sa šahovskom igrom kad na ploču dodamo još koji
"singularitet"? Očito, kad je broj singulariteta 0 imamo cilindričnu ploču kod koje je igra drugačija nego kod
möbiusove. Također, iz modela načinjenog od papira vidimo da ovakvo dodavanje singulariteta odgovara
preokretanju rubova pravokutnika prije njihovog lijepljenja kojim se dobiva geometrijski objekt kojemu ovakva projekcija sa singularitetima odgovara. Dakle problem "dodavanja singulariteta" odgovara problemu igre koju smo gore greškom definirali, a koji možemo formulirati na slijedeći način Odgovara li ta igra "šahu na cilindru", s tim da je raspored figura "poprečan" (od jednog ruba cilindra do drugog), a ne uzdužan (uzduž
oboda cilindra) kao kod "okruglog šaha" definiranog u napomeni (3)? Drugim riječima, je li za igru samu
svejedno odvija li se ona na "običnom" cilindru ili na onome koji je preokrenut četiri, odnosno paran broj puta?
Intuitivno možemo zaključiti da dvodimenzionalno biće koje bi živjelo u jednom takvom prostoru ne bi moglo
primjetiti da je njezin "ambijent" četiri puta "preokrenut" u trećoj dimenziji, a jedan argument bio bi i taj što
projekcija normalnog cilindra čiju smo jednu polovicu "zavrnuli za 180o također ima 2 "singulariteta", no tu bi
tvrdnju trebalo dokazati strogo.
Primijetimo da bi ovo značilo da preokretanjem rubova cilindra prije njihovog lijepljenja, odnosno dodavanjem
singulariteta na kružni vijenac kao dvodimenzionalnu projekciju šahovske ploče nije moguće dobiti neku novu
šahovsku igru osim spomenute dvije a to su cilindrični i möbiusov šah. U suprotnom, umjesto te dvije imali
bismo ukupno 218 = 262144 varijanti šahovske igre.
(Pitanje je može li se ovdje proći bez definiranja pojma "šahovske igre".)
4