Kada se povede reč o još nerešenim problemima u fizici, ljudi najčešće pominju nekompletnost našeg razumevanja elementarnih čestica, prirodu gravitacije i nesimetriju materije i antimaterije, brzinu širenja svemira i ulogu tamne materije, usmerenost strelice vremena, itd. Ukratko, govori se o fenomenima koji se dešavaju na ekstremno malim ili ekstremno velikim rastojanjima, fenomenima koje obično proučavaju kvantna mehanika i teorija gravitacije, a koje savremena fizika tek treba detaljno da objasni. Medjutim, problem turbulencije je težak i nerešen problem u klasičnoj fizici, koji su mnogi veliki naučnici u nekom trenutku svoje karijere pokušavali bezuspešno da reše.

Prilikom jednog predavanja, 1936. godine, Sir Horace Lamb je rekao: Ja sam star čovek, i kada odem na nebo očekujem da dobijem odgovore na dva pitanja: pitanja formulacije kvantne elektrodinamike i pitanja prirode i mehanizma turbulencije. Što se prvog pitanja tiče, imam optimistička očekivanja. Oko 20 godina kasnije, problem kvantne elektrodinamike je rešen – Fejnman, Švinger i Tomonaga su dobili Nobelovu nagradu za to rešenje - ali problem turbulencije je i danas ostao nerešen i misteriozan. Za njega je Fejnman rekao da je to verovatno najznačajniji nerešen problem u klasičnoj fizici, a Clay matematički institut nudi nagradu od milion dolara za njegovo rešenje. Šta je to problem turbulencije i zašto je on tako težak? O tome je ovaj blog.

Fenomen turbulencije, ili neravnomernog i uzburkanog toka fluida, svi mi svakodnevno vidimo. Ako polako puštamo vodu iz česme, tok je ravnomeran (ili laminaran, kako se to tehnički kaže), ali kada dovoljno pojačamo mlaz, tj. brzinu toka vode, tok postane uzburkan i nestalan. Za takav tok se kaže da je uznemiren, ili turbulentan. Često se dešava da nas, tokom vožnje avionom, pilot upozori da se pred nama nalazi turbulencija i da je potrebno da se vežemo. Kad naidje na turbulenciju u atmosferi, avion počinje da poskakuje i da se trese kao da ide po krupnoj kaldrmi. Ponekad se dešava da putnici budu povredjeni tokom takve vožnje.

Turbulentni tok fluida (tečnosti i gasova) može da se dešava na malim skalama (tok iz česme, recimo) ili na veoma velikim skalama (atmosferske pa i kosmičke dimenzije) - postoje turbulencije opsega veličina od manjeg vihora do uragana. Turbulentan tok se pojavljuje ne samo na otvorenim prostorima (u potocima ili rekama, na primer), već i u cevima (kod naftovoda, recimo), krvnim sudovima, itd. Prelazak iz laminarnog u turbulentan tok se lepo vidi na ovoj slici

Medju prvima koji su proučavali ovaj fenomen je Leonardo Da Vinči koji je naslikao oblik protoka vode pored različito postavljenih prepreka u odnosu na pravac kretanja tečnosti

On je razumeo da se iza široko postavljene prepreke stvaraju vrtlozi koji karakterišu turbulentni tok i to je predstavio na gornjem delu slike. Tačan mehanizam i trenutak nastajanja ovih vrtloga, njihova veličina, energija koja se u njima nalazi i statističke osobine takvog toka je upravo problem turbulencije na koji klasična fizika za sada nema precizne odgovore.

Osnovni uslov za nastanak turbulencije je dovoljno brz tok fluida. Naime, pri sporom kretanju tečnosti tok je laminaran (ravnomeran), a onda se, pri povećanju brzine toka, počinju da se stvaraju vrtlozi i priroda toka se menja. Objašnjenje za ovu pojavu je relativno jednostavno: osnovne sile koje deluju prilikom strujanja tečnosti su inercijalna sila i sila unutrašnjeg trenja (viskoznosti) izmedju slojeva u kretanju. Kada je brzina toka relativno mala, jačina viskoznih sila je dovoljna da stabilizuje i priguši fluktuacije brzine u tečnosti, i tok je laminaran. Kada se brzina poveća, inercijalne sile dominiraju nad viskoznim, i nestabilnosti u tečenju fluida se ne mogu prigušiti, fluktuacije se amplificiraju, i tok postane turbulentan. Odnos izmedju inercijalnih i viskoznih sila je bezdimenziona veličina koja se zove Rejnoldsov (Reynolds) broj - ovaj broj je, grubo uzevši, srazmeran brzini toka fluida. Na osnovu svega gore rečenog sledi da pri malim vrednostima Rejnoldsovog broja tok fluida je ravnomeran, a kad Rejnoldsov broj premaši neku odredjenu vrednost, i tok postaje turbulentan.

Koja tačno treba da bude vrednost Rejnoldsovog broja da bi nastala turbulencija u nekom toku? Odgovor na ovo zavisi od prirode fluida (njegove viskoznosti, na primer), oblika, veličine i geometrije suda kroz koji se protok odvija, veličine predmeta koji se kreće kroz fluid, itd. Tipične vrednosti Rejnoldsovog broja su izmedju 100 i 1000 kod protoka krvi kroz krvne sudove, oko 100,000 kod leta teniske loptice, oko 4 miliona u blizini plivača, i oko 100 miliona kod leta putničkog aviona. Sledstveno, i kritična vrednost Rejnoldsovog broja (ona vrednost pri kojoj turbulencija počinje) je različita kod različitih fluida i pri različitim vrstama toka. Ovo nije ništa posebno neobično u fizici: recimo ključanje tečnosti može da se dešava u rasponu temperatura od –270 stepeni (tečni helijum) do nekoliko hiljada stepeni (razni metali, na primer), sve u zavisnosti od toga koja je tečnost u pitanju i na kojem pritisku se ključanje dešava.

Značaj Rejnoldsovog broja se ogleda još u sledećem. Početak turbulentnog toka karakteriše pojava nestabilnosti na većim prostornom skalama (gubo rečeno, pojavljuje se prvo talas nestabilnosti na većoj talasnoj dužini). Energija ove fluktuacije se širi tako što se od ovog talasa odvajaju manji talasi i vrtlozi, od njih se dalje formiraju još manji vrtlozi, i tako se raspodela energije kaskadno propagira sve do sasvim malih skala, gde se, kroz unutrašnje trenje (viskoznost), ova mehanička energija najzad eliminiše. Ili, kako je to u stihu izrazio Richardson:

Big whirls have little whirls that feed on their velocity, and little whirls have lesser whirls and so on to viscosity

(Veliki vrtlozi imaju male vrtloge koji se njihovom brzinom hrane,

I mali vrtlozi imaju manje vrtloge i tako dalje, sve do viskoznosti)

Kod razvijene turbulencije, Rejnoldsov broj nam približno daje opseg skala na kojima dolazi do vrtložnosti, tj., daje nam razmere dimenzija vrtloga koji se formiraju. Drugim rečima, prilikom trubulentnog toka, pojavljuju se vrtlozi čije se dimenzije razlikuju do na faktor od mnogo hiljada ili miliona puta. I upravo ovo je razlog zašto je rešenje problema turbulencije tako teško.

Najteži problemi (fenomeni) u fizici su oni kod koji ne postoji dominantna skala energija, već su sve skale podjednako važne za potpuno razumevanje. Jednostavno, ništa se ne sme zanemariti. Takva situacija je 1936. godine postojala i u kvantnoj elektrodinamici, ali su pomenuti Fejnman, Švinger i Tomonaga našli način da sistematski uzmu u obzir sve skale (za zaljubljenike – oni su pokazali renormalizabilnost kvantne elektrodinamike i eliminisali divergencije u njoj). Kod problema turbulencije za sada nije poznato kako bi se ta procedura obavila. Iako je u pitanju fenomen klasične fizike – amlifikacija početne mehaničke nestabilnosti toka putem raspodele te nestabilnosti sve do mikroskopskih skala – za sada niko ne zna precizne detalje ovog procesa.

Istraživanja u oblasti turbulencije su mahom eksperimentalna. Zbog važnosti ove pojave u tehnologiji, avio industriji, medicini, astronomiji, itd., postoji mnogo istraživačkih instituta koji se ovom pojavom bave. Na primer, prilikom dizajna avionskog krila, ili čak celog aviona, važno je znati brzinu optoka fluida pri kojoj turbulencija nastaje, ali se, pored numeričkih simulacija, ovde uglavnom koriste vazdušni tuneli u kojima se direktno mere potrebni parametri.

Postoje servisi koji objavljuju podatke o atmosferskim turbulencijama kako bi upozorili avione koji se u tim oblastima nalaze. Ovo je, na primer, prognoza atmosferskih turbulencija na visinama komercijalnih letova za 06. feb. 2011:

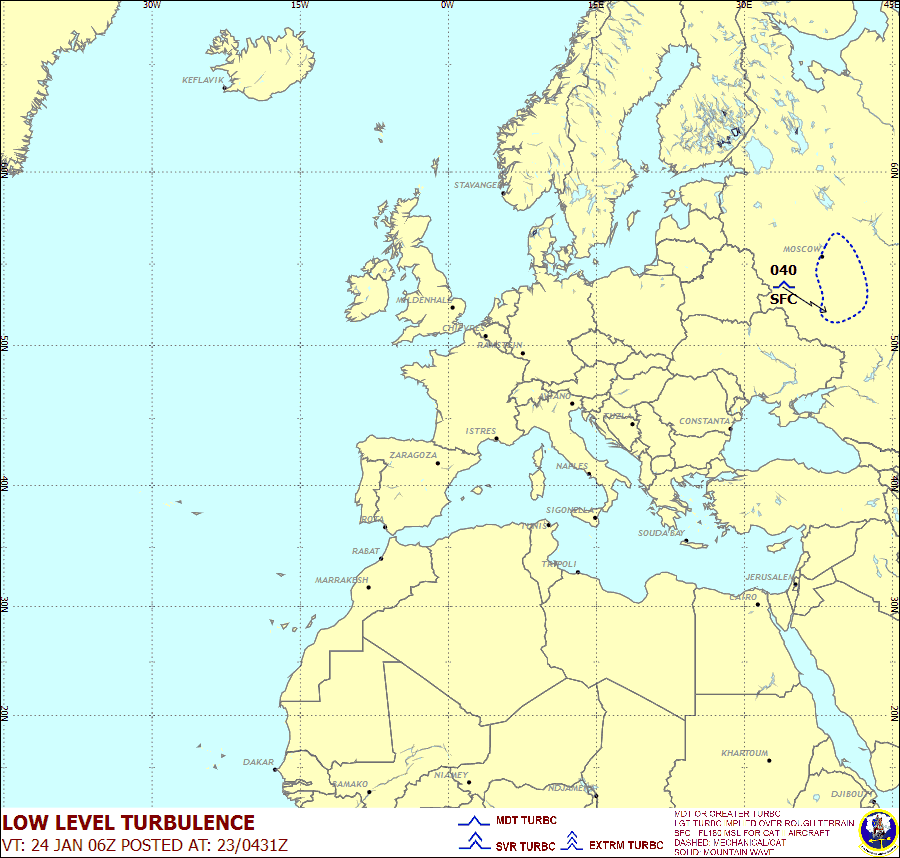
Standardni prilaz rešenju problema turbulencije je jednostavno postaviti. Pošto je u pitanju problem iz klasične fizike, napišu se jednačine kretanja fluida, tzv., Navier-Stokes jednačine i onda rešavaju pri zadatim početnim i graničnim uslovima. (Ove jednačine su, prosto rečeno, klasične jednacine Njutnove mehanike – silajednakomasaputaubrzanje – samo ovog puta zapisane za kretanje fluida). Medjutim, za sada nije poznato da li ove jednačine (u pitanju je parcijalna diferencijalna jednačina) daju turbulentna rešenja ili ne, u opštem slučaju. I za rešenje ovih jednačina, ili dokaz postojanja turbulentnih rešenja, Clay matematički institut nudi nagradu od milion dolara.

Razvojem kompjuterske tehnologije, veliki broj numeričkih pristupa je razvijen, ali mnogi realni problemi su isuviše komplikovani za moći današnjih računara. Problem turbulencije, klasičnog fenomena koji se dešava i u čaši vode i u svemiru, i na svim skalama izmedju, ostaje i dalje nerešen.

http://blog.b92.net/text/17189/Turbulencija/