4.  SPECIJALNA TEORIJA RELATIVNOSTI

Početkom XX vijeka Ajnštajnova teorija relativnosti šokirala je svijet. Ova teorija predviđala je drastične promjene zakona klasične fizike koji su vijekovima bili logični, i niko vijekovima nije sumnjao u njihovu ispravnost.

Aristotel, Njutn i svi drugi naučnici prije Anštajna vjerovali su u apsolutno  vrijeme. Smatrali su, naime, da je bespogovorno moguće izmeriti interval između dva događaja, odnosno da bi ovo vrijeme bilo isto bez obzira na to ko ga meri, pod uslovom da se koristi dobar časovnik. Vrijeme  je  bilo  potpuno  zasebno  i  nezavisno  od  prostora. Za većinu ljudi ovo bi bilo zdravorazumsko stanovište. Ali ipak, čovječanstvo je moralo da promeni svoja viđenja prostora i vremena. Iako su, kako izgleda, zdravorazumske prijedstave sasvim u redu sa stvarima kao  što su jabuke ili  planete  koje se  kreću srazmerno lagano, one potpuno gube valjanost kada su posredi stvari koje se kreću brzinom svjetlosti ili sasvim blizu nje. Najznačajnija stvar koja je doprinela nastanku Teorije relativnosti bilo je to što je Ajnštajn u fiziku uveo jedan nov pojam, pojam prostor-vremena, ovo ujedinjenje prostora i vremena, tj. posmatranje  vremena  kao jedne posebne dimenzije, ulazak u jedan nov četvorodimenzionalni prostor, dovelo je do mnogih čudnih pojava.

Teorija relativnosti sastoji se od dva glavna dela : Specijalna teorija relativnosti (STR), objavljena 1905. god i Opšta teorija relativnosti (OTR), objavljena 1916. godine. STR razmatra samo prijedmete ili sisteme koji se, jedni prijema drugima, kreću ili konstantnom brzinom (neubrzani sistemi) ili se uopšte ne kreću (brzina jednaka nuli). OTR razmatra prijedmete ili sisteme koji se jedni prijema drugima kreću sa određenim ubrzanjem (ubrzavaju ili usporavaju).

 

Naslovne strane specijalne i opšte teorije relaticnosti

4.1.   POSTULATI SPECIJALNE TEORIJE

Upoznavši se sa svim problemima nastalim tokom vršenja eksperimenata u pokušaju detekcije etera Ajnštajn je izveo dva veoma značajna zaključka. Ti zaključci poznati su kao dva osnovna postulata STR, i oni su temelj na kome se gradi cijela teorija.

Svi fizički zakoni izražavaju se u istom obliku u svim sistemima koji se kreću ravnomerno pravolinijski

Prvi postulat : Svi fizički zakoni izražavaju se u istom obliku u svim sistemima koji se kreću ravnomerno pravolinijski. Ovaj postulat prijedstavlja tzv. Ajnštajnov princip relativnosti, koji Galilejev princip relativnosti uopštava sa mehaničkih na sve fizičke zakone. Iz ovog postulata se takođe izvodi i zaključak da se eter ne može detektovati. Ajnštajn je do ovog postulata došao vrlo jednostavnim razmišljanjem.

Zamislimo čovjeka koji se  nalazi u vozu i  posmatra vagon drugog voza koji se nalazi neposredno pored njega. Ako jedan od ova dva voza krene, čovjek bi lako mogao da dođe u zabunu koji se voz zapravo kreće. Naravno, ovde je lako odrediti ko se zapravo kreće, potrebno je samo pogledati bilo koji prijedmet pored pruge, ali zamislimo sada nekog posmatrača u dalekoj budućnosti. Neka taj čovjek krene sa Zemlje na svemirsko putovanje, i neka se on konstantno kreće brzinom od 8.000 km/h u odnosu na Zemlju. Dok on tako krstari kroz prostor i izgubi Zemlju iz vida, odjednom iza sebe opaža drugu raketu, i biva iznenađen lakoćom kojim ga ova raketa prijetiče. Vozač ove druge rakete čak može da pomisli da se raketa koju zaobilazi uopšte ne kreće ! Kako će ovaj "zvijezdani putnik" da dokaže da se kreće ? Sve što

može da odredi je brzina kojom je druga raketa prošla pored njega, i ništa više od toga. Ako bi ova brzina bila 1.600 km/h može se doći do više različitih zaključaka.

Najrealniji zaključak je taj da pošto pilot zna da se on kreće brzinom od 8.000 km/h u odnosu na Zemlju, a da je druga raketa prošla brzinom od 1.600 km/h pored njega, brzina te druge rakete u odnosu na Zemlju 9.600 km/h, ali ovo ne mora biti tačno ! To isto tako može da znači da se on sada kreće brzinom od 3.000 km/h a druga raketa brzinom od 4.600 km/h u odnosu na Zemlju. Ili, ma koliko to izgledalo čudno, možda se ova druga raketa uopšte ne kreće u odnosu na Zemlju a da se posmatrač kreće unazad, brzinom od 1.600 km/h !

Brzo se dolazi do zaključka da je bez korišćenja nekog "nepokretnog" predmeta radi mjerenja brzine posmatrača nemoguće reći ko se kreće a ko miruje, ako neko uopšte miruje. Nemoguće je napraviti neki instrument koji bi pokazivao da li se posmatrač u odnosu na nešto kreće ili ne. U stvari ako bi se posmatrač nalazio negde daleko od svih zvijezda i planeta, bez ičega što bi mogao da koristi kao referentnu tačku za mjerenje brzine, on nikad neće saznati da li se kreće ili ne ! Ovo je bila činjenica do koje je Ajnštajn došao - svako kretanje je relativno. Nikada ne možemo govoriti o apsolutnom kretanju, već samo o kretanju u odnosu na nešto drugo. I uopšte se ne može reći da se neki prijedmet kreće tom-i-tom brzinom, već se mora reći da ima tu-i-tu brzinu u odnosu na nešto. Lako se može zamisliti razgovor koji će se odvijati negde u budućnosti između oca i njegovog sina koji uživa u putovanju kroz vasionska prostranstva. Otac upozorava sina da svoju raketu ne vozi brže od 1600 km/h, a sin mu odgovara: "U odnosu na Sunce, tata, ili na Sirijus ?" Iz ovoga se lako zaključuje zašto stacionarni eter ne može da se detektuje. Ako bi on postojao i ispunjavao cijelokupnu vasionu, morao bi da miruje, njegovo mirovanje bi bilo apsolutno, a Prvi postulat upravo kaže da ne postoji apsolutno mirovanje.

 

Brzina svjetlosti, odnosno maksimalna brzina prijenošenja interakcije, ista je u svim inercijalnim sistemima

Drugi   postulat  :  STR  kaže  da  je  brzina  svjetlosti,  odnosno  maksimalna  brzina prijenošenja interakcije, ista u svim inercijalnim sistemima. Ako bi se jedan dečak nalazio

na platformi i bacio loptu brzinom od 24 km/h to znači da bi se lopta u odnosu na njega kretala tom brzinom bez obzira da li se platforma kreće ili ne. Ako bi se platforma kretala, na primer, prijema mostu brzinom od 8 km/h a dečak baci loptu prijema mostu brzina lopte i platforme će se sabrati i dati ukupnu brzinu lopte u odnosu na most, i tom brzinom će lopta udariti u most. Ako bi se platforma udaljavala od mosta a dečak opet bacio loptu ka mostu brzina lopte u odnosu na most bila bi jednaka razlici  brzina platforme i lopte.

U malo složenijoj situaciji, gde ulogu dečaka igra neka daleka zvijezda, mosta – teleskop na Zemlji, a ulogu lopte prijeuzima svjetlosni talas koji putuje sa zvijezde do Zemlje situacija se malo komplikuje. Svjetlosni talas sa zvijezde putuje brzinom od 300.000 km/s u odnosu na zvijezdu. Ako bi se zvijezda i Zemlja približavale relativnom brzinom od 160.000 km/s, analogno situaciji sa dečakom, očekivali bi smo da se brzine sabiraju, odnosno svjetlosni talas bi trebalo da "udari" u teleskop brzinom od 460.000 km/s, i obrnuto ako se zvijezda i Zemlja udaljavaju brzine bi trebalo da se oduzimaju i daju

140.000 km/s. Na ovakav način posmatrač bi odredio dve različite brzine svjetlosti, i to je potpuno ispravno sa stanovišta Njutnove fizike, ali je u suprotnosti sa Drugim postulatom. Prijema Drugom postulatu brzina svjetlosti u oba slučaja mora da iznosi

300.000 km/s.

Iskaz ovog postulata bio je revolucionaran. Ipak, Ajnštajn ga je uzeo kao jedan od osnovnih postulata STR, bez obzira na to što je izgledalo da je u suprotnosti sa zdravim razumom, jer su svi eksperimenti navodili na taj zaključak. Vjerovalo se da je to jedan od osnovnih zakona vasione. Kako su ova dva postulata bila u takvoj suprotnosti sa opštim mišljenjem tog vremena,  bilo je neophodno mnogo više od njihovog prijedstavljanja javnosti. Jer, bez dalje potpore, oni bi samo bili interesantni a ne bi dokazivali ništa: Tako su, polazeći od ovih postulata izvedene mnoge jednačine koje su ne samo objašnjavale određene fenomene, nego su omogućavale i izvesna predviđanja, koja su kasnije bila eksperimentalno vjerifikovana. To je ustvari najstrožija provjera svake teorije: ne samo da omogući zadovoljavajuće objašnjenje svih zagonetki nekog problema, nego da učini i potpuno nova i drugačija predviđanja koja će tek kasnije biti eksperimentalno potvrđena.

Da bi se prijemostila praznina između ovih postulata, koji su sami po sebi apstraktni, i jednačina koje vode do potvrde i praktičnih primena teorije, postulati su morali biti ugrađeni u fizičku situaciju podložnu eksperimentalnoj provjeri. Kako se postulati odnose na prijedmet koji se kreće konstantnom brzinom u odnosu na posmatrača i na ponašanje svjetlosnih talasa, ovo se najbolje može postići ako zamislimo posmatrača koji "opisuje" prijedmet koji se kreće konstantnom brzinom u odnosu na njega. Ponašanje svjetlosnih talasa će uticati na opis jer je refleksija svjetlosnih talasa od prijedmeta do posmatrača ono što omogućava posmatraču da vidi i opiše

prijedmet. Posmatračev "opis" prijedmeta sastojaće se od fizičkih karakteristika koje se

mjere posmatračevim instrumentima (npr. dužina, masa, energija, vrijeme...)

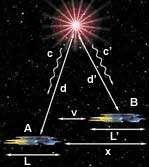
Predviđanja numeričkih vrednosti vrednosti ovih karakteristika u skladu sa STR stavljaju se u matematički oblik da bi mogla da se uporede sa stvarnim mjerenjima. Ako pretpostavimo da se dve identične rakete A i B kreću jedan prijema drugoj konačnom brzinom. Obe rakete su oprijemljene najelementarnijim naučnim instrumentima, lenjirom i časovnikom, koji su prijethodno upoređeni tako da se zna da su instrumenti u raketi A identični instrumentima u raketi B. Analiza počinje u trenutku kad B prolazi pored A, njihovi časovnici pokazuju isto vrijeme, i u tom trenutku događa se eksplozija obližnje supernove. Ni raketa A ni raketa B još nisu svesne da je zvijezda eksplodirala, jer svjetlosni talasi još nisu stigli do njih. Posle kraćeg vremena svjetlosni talasi nastali prilikom eksplozije stižu do raketa A i B koje će u tom trenutku biti na rastojanju x.

Prijema II postulatu posmatrači na A i B vide svjetlosne talase koji dolaze istom brzinom u odnosu na njih, tako da ako c prijedstavlja brzinu svjetlosnog talasa za A, a c' za B, onda se može reći da je c=c'. Sada se unesu rastojanja d i d' (između zvijezde i posmatrača) i vremena koja pokazuju njihovi časovnici t i t', i analiza produži da bi se uračunalo njihovo međusobno rastojanje, njihova relativna brzina, njihova vremena, brzina svjetlosti, itd. Jednačine koje se dobijaju nazivaju se jednačine Lorencovih transformacija, jer je Lorenc prijethodno došao do istih jednačina na osnovu svoje teorije. Koristeći jednačine Lorencovih transformacija možemo sada predvideti rezultate koje će posmatrač sa jedne rakete dobiti za masu, dužinu i td. druge rakete. Kako postulati sadrže rezultate koji su u suprotnosti sa svakodnevnim iskustvom, rezultati koji se dobijaju na osnovu Lorencovih transformacija mogu biti neočekivani i naizgled čudni. Razlog što se Teorija relativnosti, uopšte uzev, smatra neshvatljivom, nije to što je teško razumeti njene rezultate, nego što je u njih teško povjerovati.

4.2.   KONTRAKCIJA DUŽINE

Ako bi posmatrač na raketi A bio u mogućnosti da izmeri dužinu rakete B kada se one jedna prijema drugoj kreću brzinom v, matematički rezultat će predviđati da će B izgledati kao da se skratila, a njena dužina biće data formulom :

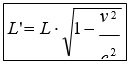
gdje je L' dužina koju A dobija za B, a L je stvarna dužina B, v njihova relativna brzina, a c brzina svjetlosti.

Ako bi rakete A i B imale dužinu od po 5 metara kada jedna u odnosu na drugu miruju. Kada se rakete udaljavaju brzinom od 150.000 km/s onda se na  osnovu jedn. (1) određuje da je prividna dužina rakete B, mjerena sa A, 4,33 metara. Ako bi se udaljavale brzinom od 260.000 km/s onda će gledano sa rakete A dužina rakete B biti približno 2,5 metara. Ista ova formula važi i ako posmatrač iz rakete B meri dužinu rakete A. Na rezultat ne utiče to da li se rakete udaljavaju jedna od druge ili se približavaju. Rezultat zavisi samo od njihove relativne brzine.

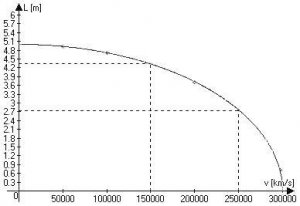Ako bi posmatrač na reketi A mjerio dužinu svoje rakete bez obzira na kretanje rakete B, on će uvijek dobiti da je dužina njegove rakete 5 metara, jer se rakete ne kreće u odnosu na samu sebe. Isto važi i za posmatrača u raketi B, za njega će dužina rakete B uvijek iznositi 5 metara. Ovaj efekat kontrakcije dužine može se jednostavno iskazati: uvijek kad se jedan posmatrač kreće u odnosu na drugog, bez obzira da li se približava ili udaljava, obojici će izgledati da se onaj drugi skratio u pravcu kretanja. Međutim, nijedan posmatrač neće zapaziti nikakvu promenu u svom sistemu. Efekat kontrakcije dužine zapaža se samo pri  brzinama koje su približne brzini svjetlosti. Kako su skoro sve brzine poznate na Zemlji, u svakodnevnom životu, nemoguće je zapaziti efekat  kontrakcije.  Ako  bi  se na primer avion kretao brzinom od 1.200 km/h u odnosu  na  posmatrača,  na  osnovu  jednačine  (1)

može se izračunati da će se on skratiti za nekoliko milionitih delova milionitog dela centimetra, otprilike za priječnik jednog atomskog jezgra. Ovako mala skraćenja nemoguće je detektovati ni najsavršenijim instrumentima, a kamoli golim okom.

4.3.   PORAST MASE SA BRZINOM

Prijetpostavimo sada da rakete A i B imaju jednaku masu kada su na Zemlji i kada su jedna prijema drugoj u relativnom mirovanju. Neka masa raketa iznosi po 1.000 kg. Ako posmatrač iz rakete A meri masu rakete B kada se one relativno kreću, videće da se masa rakete B povećala i da je njen iznos dat formulom :

 

gde je m' vrednost koju A dobija za masu B, m je prvobitna masa B ili, kako se drugačije ona naziva, masa u mirovanju, v je njihova relativna brzina, a c brzina svjetlosti. Na osnovu jednačine (2) dolazi se do zaključka da ako rakete A i B imaju masu od po 1.000 kg dok miruju na Zemlji, onda će kad se budu kretale relativno brzinom od 150.000 km/s izgledati da B ima masu od 1.200 kg posmatrano iz rakete A. Pri brzini od 260.000 km/s posmatrač iz rakete A izmeriće da B ima masu od oko 2.000 kg !

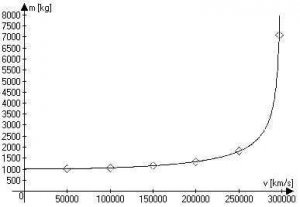Ako bi posmatrač iz rakete B takođe merio masu rakete A dok se one relativno kreću jedna u odnosu na drugu, zaključio bi da se i masa rakete A povećava saglasno formulu (2). Ako posmatrači u raketi A i B mjere masu svoje rakete oni će uvijek dobiti da masa njihove rakete iznosi tačno 1.000 kg, nezavisno od toga da li se raketa kreće ili ne, jer se ona sigurno ne kreće u odnosu na samu sebe. Kao slikovit primer porasta mase sa brzinom može se navesti brod koji plovi okeanom. Brod za sobom uvijek povlači izvesnu količinu vode. Što brže plovi, više vode će povlačiti za sobom. Zbog toga izgleda kao da brod povećava svoju masu što brže plovi, jer voda koju povlači za sobom kreće se zajedno sa brodom i postaje deo brodskog tovara. Treba napomenuti i to da porast mase ne znači da se prijedmet povećao u smislu fizičkih dimenzija (dužina, širina. visina), čak štaviše ne samo da se prijedmet nije povećao on je postao manji !

4.4.   SABIRANJE BRZINA

Neka se posmatraču istovremeno približavaju voz i automobil, i to oba brzinom od po 100 km/h u odnosu na posmatrača. Prijema tome, ako bi posmatrač merio brzinu voza i automobila dobio bi da ta brzina iznosi tačno 100 km/h. I obrnuto ako bi mašinovođa ili vozač automobila merili svoju brzinu u odnosu na posmatrača dobili bi isti rezultat. Ali, ako bi mašinovođa izmerio svoju brzinu u odnosu na automobil dobio bi da ona iznosi 200 km/h, jer se i voz i automobil kreću u odnosu na nepokretnog posmatrača brzinom od 100 km/h. Isto važi i za vozača automobila, i on se u odnosu na voz kreće brzinom od

200 km/h. Ovakve situacije su vrlo česte u svakodnevnom životu i redovno se koristi jednačina (3) :

 

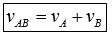
gde je vAB relativna brzina kojom se A kreće u odnosu na B (tj. brzina voza u odnosu na automobil, ili obrnuto), vA i vB je brzina A, tj. B, u odnosu na posmatrača.

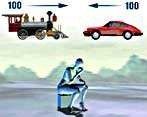Ako bi se posmatrač sada našao u sličnoj situaciji samo što bi umesto voza posmatrao svemirski brod A koji se kreće brzinom svjetlosti, a umesto automobila drugi svemirski brod  B  koji  bi  putovao  brzinom  jednakoj  polovini  brzine svjetlosti on bi lako odredio brzine ova dva svemirska broda. Piloti u brodovima takođe lako određuju svoje brzine u odnosu na posmatrača, ali šta će se desiti kada pilot jednog broda, npr. broda B, proba da odredi svoju brzinu u odnosu na drugi brod A ? Vođen prijethodnom logikom od bi dobio da brzina broda B u odnosu na A iznosi 1,5c, tj 450.000 km/s. Ako bi brzina broda B u odnosu na posmatrača bila 0,99999...c i pilot sada proba da odredi brzinu u odnosu na brod A on bi trebalo da dobije da je brzina 1,99999...c ali prijema STR ne važi jednačina (3) i relativna brzina broda B u odnosu na brod A biće jednaka brzini svjetlosti u oba ova slučaja ! Specijalna teorija relativnosti daje jedan novi zakon za određivanje relativnih brzina i taj zakon iskazan je formulom:

gde su vA i vB relativne brzine kojima se A i B kreću prijema nepokretnom posmatraču, a c je brzina svjetlosti.

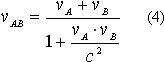
Ako bi na primer uzeli da brzine vA i vB iznose po 160.000 km/s, relativna brzina tijela A prijema telu B bila bi 250.000 km/s prijema jednačini (4), a ne 320.000 km/s kako daje jednačina (3). Lako se uočava da ovde dve jednačine daju dve različite vrednosti za jednu istu stvar pa prijema tome ne mogu obe da budu ispravne ! Za sve praktične primene jednačina (3) se može smatrati ispravnom kada su brzine znatno manje od brzine svjetlosti, ali kada su brzine približne brzine  svjetlosti  mora  se  koristiti  jednačina  (4).  Videli  da

razlika u vrednostima koje daju ove dve jednačine pri brzinama od 160.000 km/s iznosi

70.000 km/s, ali ako bi brzine bile na primer 160 km/h, rezultat koji daje jednačina (3) razlikovao bi se od rezultata jednačine (4) za oko dva milionita dela santimetra.

4.5.   MAKSIMALNA MOGUĆA BRZINA

Od svih predviđanja koja proizilaze iz STR, vjerovatno je najčudnije ono da postoji određena brzina prijeko koje se ništa ne može kretati. Koja je to brzina lako se može naslutiti iz jednačine (1), koja određuje skraćenje prijedmeta sa brzinom. Na osnovu te jednačine vidi se da prijedmet postaje sve kraći i kraći kako se brzina povećava. Ako brzina postaje sve veća i veća prijedmet će se sve više smanjivati, kada njegova brzina bude približna brzini svjetlosti dužina će biti približna nuli, u onom trenutku kada brzina postane jednaka brzini svjetlosti prijedmet će nestati. Ako prijetpostavimo da brzina nastavi da raste. Ako bi brzina bila dva puta veća od brzine svjetlosti, tj. v=2c, pod korenom se dobija –3, odnosno dužina prijedmeta je sada prvobitna brzina pomnožena sa korenom iz –3. Kako je kvadratni koren iz negativnog broja imaginaran broj to znači da će i dužina prijedmeta biti imaginarna, tj. prijedmet neće postojati.

Na osnovu jednačine (2) moguće je odrediti šta će se dešavati sa masom prijedmeta kada se njegova brzina približava brzini svjetlosti. Sa porastom brzine, izraz pod korenom se smanjuje. Kako vrednost razlomka raste kako mu se imenilac smanjuje, masa prijedmeta raste. Ako brzina v toliko poraste da se izjednači sa brzinom svjetlosti, onda će imenilac postati jednak nuli, što znači da će masa postati beskonačno velika.

Iz ovoga moguće je izvući samo jedan zaključak – da je brzina svjetlosti maksimalna moguća brzina. Nijedan prijedmet ne može putovati brže od svjetlosti, jer ne samo što mu se dužina smanjuje na nulu nego će i njegova masa postati beskonačno velika. Ustvari, tačnije je reći da se materijalni prijedmeti koji su poznati u svakodnevnom životu nikada ne mogu kretati brzinom svjetlosti jer bi njihova masa tada postala beskonačno velika, što znači da bi bilo potrebno beskonačno mnogo energije da se dovedu do te brzine. Na osnovu ovoga vidi se zašto je neophodna jednačina (4). Ako bi koristili samo jednačinu (3) u nekim slučajevima relativna brzina dva tijela mogla bi da bude veća od brzine svjetlosti, što je nemoguće. Bez obzira na brzinu kojom se dva prijedmeta kreću u odnosu na nekog posmatrača, njihova relativna brzina uvijek je manja od brzine svjetlosti.

4.6  EKVIVALENTNOST MASE I ENERGIJE

Najznačajnije predviđanje STR bilo je to da je srazmerno mala količina mase ekvivalentna ogromnoj količini energije. Danas je dobro poznato da je prvi ubedljiv dokaz ovog predviđanja bila eksplozija prve atomske bombe kod Alamogorda (Nju Meksiko, SAD) 16. Jula, 1945. godine. Kako STR predviđa da sa porastom brzine raste i masa tijela, zaključuje se da i energija tijela mora da raste jer masivniji prijedmet ima veću energiju od lakšeg ako su im brzine jednake. Moguće je pokazati da je dodatna energija, koja je povezana sa dodatnom masom, jednaka porastu mase pomnoženim sa kvadratom brzine svjetlosti. Na osnovu ovakvog razmišljanja Ajnštajn je zaključio da je sva masa povezana sa energijom, a ta veza data je njegovom čuvenom formulom :

E = mc 2

gde je E ekvivalentna energija, m masa tijela, a c brzina svjetlosti. Drugim rečima, ako bi se masa bilo koje supstance prijetvorila u energiju, bez ostatka, iznos energije koji će se dobiti dat je formulom (5). Na primer ako bi se u jednačinu uvrstio 1 kg uglja, za energiju se dobija 250 milijardi kilovat-časova, to je približno jednako energiji koju proizvedu sve elektrane u SAD za Mjesec dana. Kafena kašičica ugljene prašine bila bi dovoljna da najveći brod koji plovi okeanima nekoliko puta prijeđe rastojanje od Njujorka do Evrope i natrag. Iz svakodnevnog života svima je poznato da se prilikom sagorevanja uglja oslobađa neuporedivo manja količina energije. Da li to ukazuje na neispravnost STR ? Prilikom običnog sagorevanja uglja energija koja se oslobađa se energija koja nastaje kao rezultat hemijskog procesa, dolazi samo do prijeuređivanja i novog vezivanja atoma i molekula, ali ne dolazi do merljive konvjerzije mase u energiju jer se ugalj prijetvara u čađ, pepeo, dim, a ne nestaje. Kad bi se svi ovi krajnji produkti izmerili njihova ukupna masa opet bi bila 1 kg. Upoređivanjem količine energije koja bi nastala pri prijetvaranju 1 kg uglja u energiju i običnog sagorevanja iste mase uglja, vidi se da se pri sagorevanju oslobađa tri milijarde puta manje energije. Naravno, proces u kome se znatna količina mase prijetvara u energiju je potpuno drugačije prirode od običnog sagorevanja.

4.7  VRIJEME U SPECIJALNOJ TEORIJI RELATIVNOSTI

Specijalna teorija relativnosti je podstakla mnogo drugačiji način razmišljanja o prostoru. Pokazala je da dužina, masa i energija nego tijela nisu stalne već da su ove veličine usko povezane sa brzinom. Ali, Ajnštajnova Teorija je pojam vremena uvela kao novu "dimenziju". Možda najveći doprinos STR bio je vezan za doprinos koji je dala drugačijem shvatanju pojma vremena.

Kako se prijema STR ponaša vrijeme može se videti na istom primeru koji je i do sada korišćen. Časovnici na raketama A i B pokazuju isto vrijeme u trenutku kada su rakete jedna pored druge, neka je, na primer, u tom trenutku bilo 12 časova. Ovo početno vrijeme može se nazvati nultim vremenom.

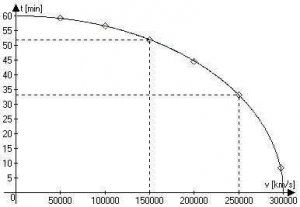
Kako vrijeme prolazi, rastojanje između A i B se povećava pošto se rakete kreću relativno jedna u odnosu na drugu, i posle nekog konačnog vremenskog intervala rastojanje između rakete A i rakete B iznosiće x. Ako posmatrač na A tada pogleda na svoj časovnik i uporedi sa časovnikom na B, biće iznenađen zato što ova dva časovnika ne pokazuju isto vrijeme – onaj koji se nalazi na B kasni. Ovu pojavu predviđa STR jer matematički rezultati pokazuju da se vrijeme koje pokazuju časovnici ponaša prijema jednačini :

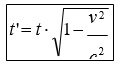
gdje je t' vrijeme koje posmatrač A "vidi" na časovniku B, a t vrijeme koje posmatrač A očitava na svom časovniku. Ako se prijetpostavi da je relativna brzina kojom se raketa A i B udaljavaju 150.000 km/s onda će posmatraču na raketi A izgledati da časovnik na B radi za približno 10% sporije, tj ako onaj na A pokazuje 1 čas, časovnik na B će pokazivati 54 minuta; uvijek kad posmatrač na A pogleda svoj časovnik, onaj na raketi B će pokazivati 9/10 tog vremena. Ako bi relativna brzina bila 260.000 km/s onda se prijema jednačini dobija da bi časovnik na B pokazivao samo polovinu vremena koje pokazuje časovnik A. Što je relativna brzina veća časovnik na raketi B će se kretati sve sporije i sporije, bez obzira da li se rakete približavaju ili udaljavaju. Naravno, i ako bi posmatrač koji putuje raketom B uporedio vrijeme na svom časovniku i onom u raketi A, dobio bi da časovnik u raketi A kasni, a to kašnjenje bi takođe bilo dato jednačinom (6).

Ovaj efekat kašnjenja časovnika u STR se naziva dilatacija vremena i ona nastaje onda kada se dva posmatrača kreću relativno jedan prijema drugom konstantnim brzinama, tada svakom od njih izgleda da časovnik onog drugog kasni. Iz ovih primera može se

izvesti zaključak da razlog časovnici A i B kasne jadan u odnosu na drugi nije samo u specifičnom ponašanju svjetlosnih talasa već i uzrok toga i izvestan vremenski interval neophodan svjetlosnim  talasima  da  putuju od jednog do drugog časovnika. Efekat dilatacije vremena odgovoran je za jedan potpuno drugačiji pogled na vrijeme od onog koji korišćen ranije. Ranije se uvijek smatralo da je vrijeme isto za sve posmatrače, ma gde se oni nalazili i ma kako se kretali, vrijeme je proticalo jednakom brzinom za svaku osobu i za svaki prijedmet u cijeloj vasioni. Vrijeme je bilo apsolutno. STR je pokazala

da ovo shvatanje nije bilo tačno. Ona je pokazala da vrijeme protiče različitom brzinom za dva posmatrača koji se, jedan u odnosu na drugog, nalaze u relativnom kretanju.

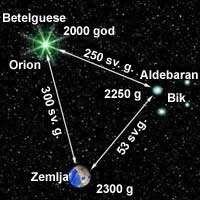Međutim, STR je pokazala da je vrijeme različito i za posmatrače koji jedan u odnosu na drugog miruju, ali koji se nalaze na velikoj udaljenosti jedan od drugog. Ako bi dva posmatrača, jedan koji se nalazi na Zemlji i drugi koji se nalazi u blizini zvijezde Aldebaran (u sazvežđu Taurus), posmatrali eksploziju supernove na zvijezdi Betelgeuse (u sazvežđu Orion). Rastojanje od Zemlje do zvijezde Betelgeuse iznosi 300 svjetlosnih godina, od Betelgeuse do Aldebarana je 250 svjetlosnih

godina, a Aldebarana do Zemlje rastojanje je 53 svjetlosne godine. Neka se eksplozija supernove desi na primer 2000 godine (prijema načinu kako mi merimo vrijeme na Zemlji). Ljudi na Zemlji ne bi videli blesak eksplozije te godine, jer je Betelgeuse udaljena 300 svjetlosnih godina, što znači da bi svjetlosnim talasima nastalim pri eksploziji bilo potrebno 300 godina da stignu do naše planete. To je jedini način da ljudi na Zemlji saznaju da je zvijezda uništena. S druge strane, neko u okolini Aldebarana bi istu eksploziju video 2250. godine, jer je Aldebara udaljen 250 svjetlosnih godina

od Betelgeuse. Lako se uočava činjenica da ovaj događaj nije simultan (istovremen) za

tri različita mesta, jer svako događaj posmatra u drugo vrijeme, čak se možda može reći da vrijeme putuje brzinom svjetlosti.

Pored velikih rastojanja u prostoru do razlike u simultanosti događaja može doći i pri malim rastojanjima ali onda kad su relativne brzine posmatrača približne brzini svjetlosti.

STR je pokazala da ako su dva događaja istovremena za

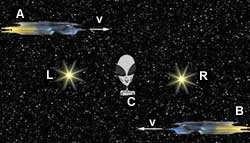
jednog posmatrača ne moraju biti istovremena za sve posmatrače, čak je moguće da i redosled događaja za različite posmatrače bude različit. Ako  se  na  primer dva posmatrača nalaze u identičnim raketama A i B  i putuju jedan prijema drugom brzinom v, koja je nešto manja od brzine svjetlosti, u odnosu na stacionarnog posmatrača C koji  se  nalazi  na  pola puta između  ove dvojice.  Na  podjednakom  rastojanju  od  posmatrača  C,

sa leve i desne strane, nalaze se i dve sijalice L i R. U trenutku kada rakete prolaze pored

sijalica one se pale.

Kada posmatrač A prođe prijed sijalice L ona će se upaliti, u istom tom trenutku pali se i sijalica R pošto je pored nje prošla raketa B. Pošto je, po prijetpostavci, rastojanje od L do posmatrača C jednako rastojanju od R do C, vrijeme koje je potrebno da svjetlost sa upaljenih sijalica L i R stigne do C je jednako, pa će događaj paljenja ove dve sijalice za posmatrača C biti simultan (istovremen). Za posmatrače u raketama A i B situacija će biti malo drugačija. Rastojanje koje treba da prijeđe svjetlost sa sijalice L je daleko manje od rastojanja potrebno svjetlosti sa sijalice R da stigne do posmatrača A. Zbog razlike u dužini potrebnog vremena posmatrač A prvo će videti da se upalila sijalica L a tek kasnije će videti paljenje sijalice R. Posmatrač u raketi B će registrovati sličnu situaciju, sa tom razlikom što će njemu izgledati da se prvo upalila sijalica R a zatim L. Ova situacija pokazuje dva događaja koja si simultana za stacionarnog posmatrača, a nisu simultana za druga dva posmatrača. Ustvari, sa tačke gledišta posmatrača A, prvo se odigrao događaj L a zatim R, a sa tačke gledišta posmatrača B događaj R je prijethodio događaju

L. Niko ne može reći koji se događaj "stvarno" odigrao prvi ili su se događaji možda

odigrali istovremeno, jer su sva tri posmatrača jednako upravu i nijedan od ova tri pogleda nema prijednosti u odnosu na druge. STR je tako pokazala neispravnost vijekovima stare ideje o istovremenosti događaja, prijema kojoj dva događaja, ako su istovremena za jednog posmatrača, moraju biti istovremena i za sve ostale posmatrače. Redosled događaja je funkcija položaja posmatrača i relativne brzine u odnosu na sve druge posmatrače. Istovremenost je relativna stvar, ne postoji apsolutno vrijeme.

Naravno treba naglasiti i to da što je veće rastojanje u prostoru između  mesta odigravanja dva simultana događaja veća će biti moguća razlika u vremenu između ta dva događaja kako ih vide različiti posmatrači pod različitim uslovima. I obrnuto, ako se rastojanje između dva "istovremena" događaja smanji do iščezavanja, tj. ako se događaji dešavaju na istom mestu , svi posmatrači, bez obzira na njihove položaje i relativne brzine, složiće se u pogledu istovrijemnosti ovakva dva događaja. Na primer, ako bi došlo do sudara dve rakete, svi posmatrači će videti taj sudar kao jedan usamljen događaj. Bilo bi smešno, a i protivno svim zakonima fizike ako bi bilo koj posmatrač tvrdio da se jedna raketa sudarila prije druge bez fizičkog uzroka.

4.7.1  Paradoks Blizanaca

Predviđanja STR o dilataciji vremena navode na neke vrlo zanimljive, a možda i zastrašujuće ideje. Efekat dilatacije vremena mogao bi da ima neke vrlo interesantne primene za vasionska putovanja. STR ne samo da predviđa da će na raketi koja se kreće relativno brzinom bliskoj brzini svjetlosti samo vrijeme proticati sporije, ona takođe predviđa da će SVI procesi biti usporeni. To znači procesi varenja hrane, biološki procesi, atomska aktivnost – sve će biti usporeno !

Ako bi na primer neki "zvijezdani putnik" u dalekoj budućnosti odlučio da krene na "godišnji odmor" na primer do zvijezde Arcturus (sazvežđe Bootes, Pastir) koja je udaljena 33 svjetlosne godine. Ako bi putovao brzinom bliskom brzini svjetlosti on će na Arcturus stići za malo više od 33 godine, ali po vremenu na Zemlji, ako bi odmah krenuo natrag na Zemlju će stići približno 66 godina nakon odlaska. Kako se raketa cijelo vrijeme kretala ogromnom brzinom u odnosu na Zemlju svi procesi na raketi biće usporeni, putniku u raketi neće izgledati da je proteklo 33 godine za put u jednom smeru, on će stići u blizinu Arcturusa otprilike baš u vrijeme ručka, a kad se bude vratio na Zemlju izgledaće mu da je prošao samo jedan dan ! Ali, ljudima na Zemlji to će biti 66 godina, ljudi na Zemlji će biti 66 godina stariji. Jedan rezultat koji predviđa STR bio je izvor velike nedoumice i izvesnog neslaganja od vremena svog prijedstavljanja. To je tzv. paradoks blizanaca ili vremenski paradoks. Prijetpostavimo da od dva blizanca jedan odlazi na putovanje do neke daleke zvijezde i natrag a drugi ostaje na Zemlji. Neka je ta zvijezda udaljena 4 svjetlosne godine od Zemlje, a da se raketa kreće prosečnom brzinom koja je jednaka 4/5 brzine svjetlosti. Ukupno vrijeme za njeno putovanje biće tada oko 10 godina. Ako uporedimo brzinu proticanja vremena za blizanca u raketi sa brzinom proticanja vremena na Zemlji, na osnovu jednačine (6) dobija se :

 

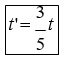
Ovo znači da iako je putovanje trajalo deset godina prijema časovniku blizanca na Zemlji, prijema časovniku onog u raketi putovanje je trajalo samo šest godina. Po povratku sa puta blizanac će shvatiti da nije ostario onoliko kolko i njegov brat koji je stao na Zemlji. Paradoks se ovde ogleda u tome da pošto su sva kretanja relativna može da se smatra da je Zemlja otišla u svemirski prostor u pravcu suprotnom od rakete i vratila se dok je raketa mirovala. Na osnovu takvog razmatranja kretanja dolazi se do suprotnog zaključka – blizanac u raketi čekaće 10 godina na povratak svog brata, koji će misliti da je u putovanju (sa Zemljom) proveo samo šest godina. Očigledno je da ova dva tumačenja ne mogu istovremeno biti tačna. Upravo ova kontradikcija prijedstavlja tzv. paradoks blizanaca. Rešenje paradoksa je vrlo jednostavno, tačnije paradoks uopšte ne postoji pošto ove dve situacije  nisu simetrične, pa nisu ni matematički reverzibilne. Razlog nepostojanja simetrije je taj što raketa na svom putovanju trpi određena ubrzanja, a prijetpostavka da Zemlja odlazi na putovanje nije ispravna jer bi u tom slučaju Zemlja morala da trpi odgovarajuća ubrzanja umesto rakete, a poznato je da se to ne dešava. STR neizbežno vodi do zaključka da će za vasionskog putnika na kružnom putovanju proći ukupno manje vremena, nezavisno od načina mjerenja, nego za ljude koji ostaju na Zemlji. Svaki putnik će se na Zemlju vratiti manje ostareo nego oni koji su

ostali da ga čekaju. Ukupan iznos usporenja vremena zavisiće od brzine rakete u odnosu na Zemlju i ukupnog prijeđenog rastojanja za vrijeme puta.

Do fizičke osnove ovakvog zaključka može se doći poređenjem onoga što svaki blizanac vidi kad posmatra svjetlosne talase primljene iz niza događaja koji se dešavaju u sistemu onog drugog. Tokom prve polovine putovanja, zbog brzine kojom se raketa udaljava od Zemlje, svjetlosni talasi događaja na Zemlji stizaće do rakete sporijim tempom, učestalošću, nego kad bi raketa mirovala. Za brzinu rakete od 4/5 brzine svjetlosti, ovo usporenje je dato formulom za tzv. relativistički Doplerov pomak, prijema kojoj će učestalost biti 1/3 od normalne. Na sličan način za vrijeme povratka blizanac u raketi posmatra događaje na Zemlji kao da se odigravaju tri puta bržim tempom. Tokom cijelog putovanja blizanac na raketi registruje događaje na Zemlji kao da se odigravaju prosečnim tempom od 5/3 (što je prosek za od jedne trećine i tri). Znači, rezultat je da blizanac na raketi zapaža da vrijeme na Zemlji protiče u proseku brže nego na raketi, pri čemu tačan odnos iznosi 5/3, zbog toga će deset godina na Zemlji biti kao šest godina na raketi.

Situacija koju vidi blizanac na Zemlji je obrnuta. On svjetlosne talase događaja koji se na raketi odigravaju tokom prve polovine putovanja prima ukupno devet godina. To je zbog toga što raketi treba pet godina Zemaljskog vremena da stigne do zvijezde i još četiri godine su potrebne svjetlosnim talasima da stignu sa udaljene rakete do Zemlje, jer se raketa nalazi na rastojanju od četiri svjetlosne godine. Tokom ovih devet godina, blizanac na Zemlji posmatra događaje tri puta sporije od normalnog tempa, u skladu sa relativističkom formulom Doplerovog pomaka. Događaje koji se odigravaju na raketi tokom povratka na Zemlju blizanac sa Zemlje će posmatrati samo poslednje, desete godine. Za vrijeme ove poslednje godine on će događaje na raketi videti kao da se odigravaju tri puta brže nego što je to normalno. Ukupan rezultat daje da će događaje koji na raketi ukupno traju šest godina blizanac na Zemlji posmatrati deset godina, odnosno u proseku će vrijeme na raketi proticati sporije nego na Zemlji. Iz ovoga se vidi zbog čega fizička situacija nije simetrična za oba blizanca i zašto je ukupno vrijeme putovanja različito za svakog od njih. Blizanac sa rakete prijeusmerava svoju brzinu na polovini svog putovanja i počinje da zapaža događaje na Zemlji ubrzanim tempom odmah nakon toga, dok blizanac na Zemlji mora da čeka još četiri godine da svjetlosni talasi događaja okretanja rakete stignu do njega prije nego što počne da prima ubrzanim tempom događaje sa rakete. Jednostavnije rečeno, zemaljski blizanac prima svjetlosne talase događaja na raketi sporijim tempom ali duže vrijeme nego blizanac u raketi one sa Zemlje. Efekat ove asimetrije je da zemaljski blizanac posmatra manje događaja koji se dešavaju na raketi, nego što blizanac na raketi posmatra događaja na Zemlji za vrijeme cijelog putovanja.

Moglo bi izgledati da su zaključci koji proizilaze iz ovakvog putovanja u suprotnosti sa predviđanjem STR da je brzina svjetlosti maksimalna brzina.  Kako  je  putovanje  dugo osam svjetlosnih godina, a raketa ga prelazi za šest godina putovanja zabeleženim na raketi, prostim izračunavanjem brzine (deljenje prijeđenog puta sa utrošenim vremenom) dobija se da brzina kojom se raketa kretala za jednu trećinu veća od brzine svjetlosti. U čemu je ovde greška ? Razlog zbog čega se javlja "prijekoračenje" brzine svjetlosti je to što raketa stvari ne prelazi rastojanje od osam  svjetlosnih  godina.  Kao  posledica brzine rakete rastojanje do zvijezde biće skraćeno za blizanca u raketi usled Ficdžerald-Lorencove kontrakcije, pa na osnovu toga korišćenjem jednačine  (1)  i numeričkih vrednosti iz ovog primera dobija se skraćeno rastojanje od  4,8  svjetlosnih godina za povratno putovanje. Deljenjem tog iznosa sa vremenom provedenim u putu, tj. sa šest godina, lako se utvrđuje da prosečna brzina stvarno iznosi 4/5 brzine svjetlosti.